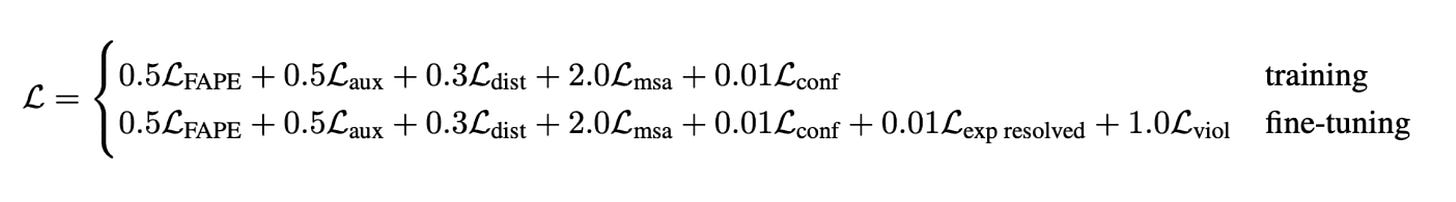AlphaFold: Protein Structure Prediction

What is protein folding and how does AlphaFold work?

Proteins are the molecular machines vital to every cell and organism, and understanding their structure is crucial for the discovery of new drugs to treat diseases or the discovery of new materials. Researchers have now made significant progress toward this goal by developing machine learning (ML) algorithms capable of accurately predicting the folded shapes of proteins and other biomolecules.

In this article, I’ll explore how protein folding works, how AlphaFold2 predicts novel protein structures, and how the newer AlphaFold3 model works. Before we begin, let’s refresh ourselves on how proteins work and fold.

Primer on Proteins

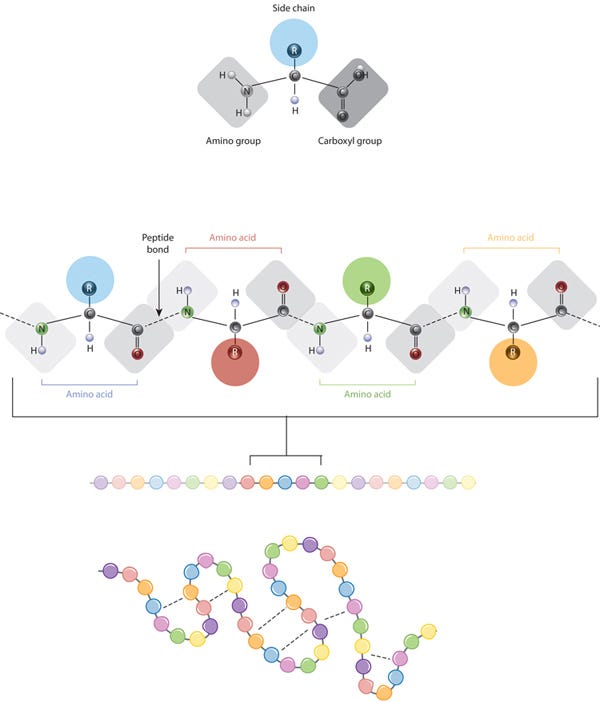
Proteins are composed of multiple amino acids (a set of 20) linked by peptide bonds. These bonds connect the amino group of one amino acid to the carboxyl group of the next.

All amino acids share a common backbone structure, which includes an amino group (NH2), a carboxyl group (COOH), and a central carbon atom (alpha carbon) bonded to a hydrogen atom and a variable side chain (R-group). The R-group is what makes each amino acid unique.

The chemistry of amino acid side chains is crucial for protein structure because these side chains can interact with each other, helping to maintain the protein's specific shape or conformation. The side chain (represented as colored circles) is the key characteristic that distinguishes each amino acid. When peptide bonds link amino acids, they form a polypeptide (protein). The polypeptide then folds into a specific shape based on the interactions (indicated by dashed lines) between the side chains of the amino acids.

A protein's sequence of amino acids determines how it folds and bonds within itself, creating its unique 3D structure. Hydrogen bonds between specific groups of amino acids lead to the formation of alpha helices and beta sheets, which make up the secondary structure. Most proteins have multiple helices and sheets.

The different folds and configurations within a single amino acid chain form the tertiary structure, while proteins with multiple chains or subunits have a quaternary structure. In summary, a protein has a primary structure (a linear chain), a secondary structure (partially 3D with some sparsity), and a tertiary structure (fully 3D and ordered).

Upon synthesis, proteins typically adopt the most energetically favorable shape, going through a series of conformational changes before stabilizing into a unique form. The stability of these folded proteins depends on numerous noncovalent bonds between amino acids and their interactions with the surrounding environment.

The Challenge: Visualizing Proteins

Despite being macromolecules, proteins are too small to be seen even with a microscope. Therefore, scientists rely on indirect methods to determine their appearance and folding. The most common technique for studying protein structures is X-ray crystallography. A key point is that reading protein sequences is relatively inexpensive and can be done directly with mass spectrometry (~$100 per sample) or indirectly through DNA genome sequencing (ranging from $100 to $1000 per sequence). In contrast, experimentally determining the 3D structures of proteins is much more costly ($100,000 to $1 million per structure) and is typically performed using X-ray crystallography or MRI.

This raises the question of whether machine learning can be used to accelerate the understanding of protein structure directly from amino acid sequences.

Evolutionary Conservation and Homologous Proteins

Proteins frequently display evolutionary conservatism, meaning similar proteins can be found across different species with slight variations in their amino acid sequences. These similar proteins are called homologues. This leads to several insights:

1. Evolutionary changes in protein sequences are often neutral, meaning they do not significantly affect protein function. Despite variations in amino acid sequences, the overall 3D structure of proteins tends to remain relatively conserved.

2. To compare homologous proteins from different species, scientists use a technique called multiple sequence alignment (MSA). In MSA, protein sequences from various species are aligned in a 2D table format, placing corresponding amino acid residues in the same columns and species in different rows. This allows researchers to identify conserved regions, understand evolutionary relationships, and infer functional significance based on sequence conservation.

In summary, proteins that perform similar functions in different species often have similar overall structures, even if their amino acid sequences differ.

AlphaFold2: Overview of Architecture

At a high-level, AlphaFold2: 1. identifies similar sequences to the input, 2. extracts relevant information using a specialized NN architecture, and 3. uses this information to produce a protein structure through another NN.

1. Initially, the AlphaFold 2 system uses the input amino acid sequence to search several protein sequence databases and creates a multiple sequence alignment (MSA). An MSA identifies sequences that are similar, but not identical, which have been found in living organisms. This process helps determine which parts of the sequence are more prone to mutations and detects correlations between them. AlphaFold 2 also searches for proteins with structures similar to the input (called “templates”) and constructs an initial structural model known as the “pair representation,” which predicts which amino acids are likely to be in contact with each other.

2. In the next phase, AlphaFold 2 processes the MSA and the templates through a transformer. A transformer (which I’ll explain shortly) can be thought of as a method that quickly identifies the most informative pieces of information. This stage refines the representations of both the MSA and the pair interactions by iteratively exchanging information between them. Improving the MSA representation enhances the network’s understanding of the geometry, which in turn refines the MSA model. This process is represented as blocks that are repeated iteratively, with 48 blocks used in the published model.

3. The final part of the process is the structure module. This component uses the refined MSA and pair representations to construct a three-dimensional model of the protein structure. It generates a static, final structure in a single step. The output is a detailed list of Cartesian coordinates representing the positions of each atom in the protein, including side chains.

Preprocessing

AlphaFold2 has a preprocessing pipeline in which using the input sequence, generates a multiple sequence alignment (MSA) and a list of templates.

A core component here is MSA. In an MSA, the sequence of the protein whose structure we intend to predict is compared across a large database (such as UniRef or metagenomics). The principle here is that if two amino acids in a protein are in close contact, a mutation in one will likely be followed by a mutation in the other. This maintains the protein's structure and is known as co-evolution or covariation. Conversely, if two regions of a protein evolve independently, they are likely not in direct contact.

Another key aspect is finding templates. Although proteins mutate and evolve, their structures tend to remain similar. For instance, the structure of four different myoglobin proteins (as seen below) from different organisms may look almost identical at first glance, but their sequences have significant differences. For example, the protein on the bottom right shares only about 25% of its amino acids with the protein on the top left. This concept is used to find templates, which are proteins with structures similar to the input protein.

The Evoformer Module

When AlphaFold predicts the 3D structure of a protein, it generates a set of "pair representations." Each pair of amino acid residues in the protein, regardless of their distance, is represented individually. This allows us to encode the co-evolutionary relationships between amino acid residues based on the MSA. This data can ultimately be interpreted as the relative positions and distances between amino acid residues.

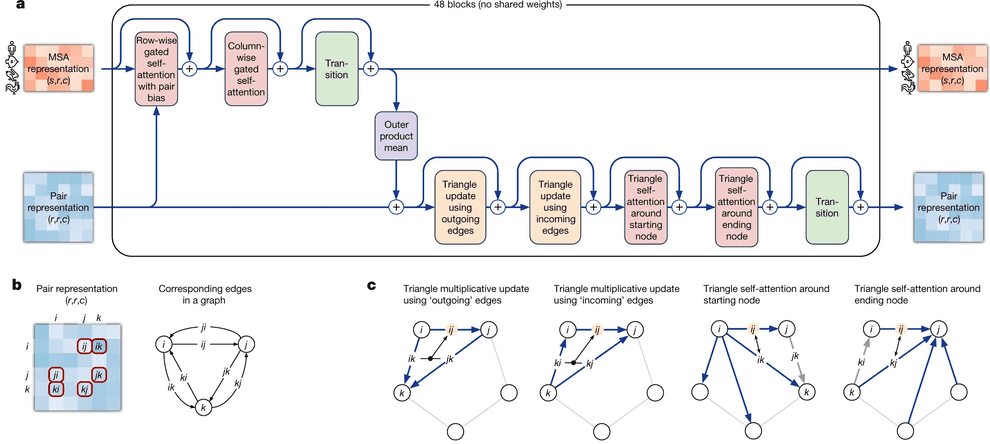
AlphaFold2 employs a neural network called Evoformer, which interprets and updates both the MSA and the pair representations.

The central idea behind Evoformer is the continuous flow of information throughout the network. In Evoformer, during each cycle, the model uses the current structural hypothesis to improve the MSA assessment, which then leads to a new structural hypothesis, and this process repeats. Both sequence and structure representations exchange information until the network reaches a robust prediction.

For instance, if you observe a correlation between a pair of amino acids, A and B, in the MSA, you might hypothesize that A and B are close together. This assumption is incorporated into your structural model. Reviewing this model, you might infer that if A and B are close, then C and D should also be close. This generates another hypothesis, which can be validated by looking for correlations between C and D in the MSA. Repeating this process multiple times helps build a comprehensive understanding of the structure.

In the diagram below, the transformer for the MSA (“MSA Transformer” in diagram) identifies a correlation between two MSA columns, each corresponding to a residue. This information is passed to the pair representation, which then identifies another possible interaction. In the subsequent diagram, the information is fed back to the MSA. The MSA transformer receives input from the pair representation and detects another significant correlation between two columns. This back-and-forth between MSA and pair representation is key.

Attention and transformer architecture

The neural network at the core of AlphaFold2 utilizes transformer architecture and the attention mechanism. Here’s a brief explanation of these concepts. Feel free to skip this section if you are already familiar with attention mechanisms and transformers.

Attention

Imagine we have a key-value database (similar to a Python dictionary), and we provide a query (a key that contains typos).

We want the database to compare the query with each key and return a value, which is a weighted average of the values, where the weight of each value indicates the probability that the user intended that specific key.

We can interpret these similarities as probabilities. To normalize the similarities between queries and keys so their weights sum to 1, we use the Softmax function.

There’s a few nuances to note here for attention. Attention mechanisms typically handle a list of queries rather than a single query, compare them to keys, and return a weighted average of values for each query.

In most cases, keys, queries, and values are vectors. We measure their similarity using methods like cosine distance or the dot product.

For instance, the inputs to an attention mechanism could be lists of three queries, three keys, and three values, with each individual query, key, and value represented as an embedding vector, such as one with a dimensionality of 128. Here’s how you could implement Attention in PyTorch (source):

import torch
import torch.nn as nn
import torch.nn.functional as F


def attention(query, key, value, mask=None, dropout=None):
    """Compute 'Scaled Dot Product Attention'.
    
    Mostly stolen from: http://nlp.seas.harvard.edu/2018/04/03/attention.html.
    """

    # MatMul and Scale
    d_k = query.size(-1)
    scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)
    
    # Mask (optional)
    if mask is not None:
        scores = scores.masked_fill(mask == 0, -1e9)
    
    # Softmax
    p_attn = F.softmax(scores, dim = -1)
    
    # MatMul
    if dropout is not None:
        p_attn = dropout(p_attn)
    
    return torch.matmul(p_attn, value), p_attn

Multi-head attention

Multi-head attention involves performing computations such that the attention module iterates multiple times, organizing into parallel layers known as attention heads. Each head processes the input sequence and the corresponding output sequence element independently.

If we have key and value matrices, we can transform the values into h sub-queries, sub-keys, and sub-values, which independently pass through the attention mechanism. These are then concatenated into a single head and combined with a final weight matrix.

The learnable parameters in this process are assigned to the head, and this setup is known as the Multi-Head Attention layer. This mechanism forms a single multi-head attention block, which is a unit of a transformer network.

In the problem of protein folding, stacking multiple layers of multi-head attention allows us to identify more complex and high-level relationships between protein amino acid residues. Here’s an example implementation (source):

import torch
import torch.nn as nn
import torch.nn.functional as F


class MultiHeadedAttention(nn.Module):
    """Mostly stolen from: http://nlp.seas.harvard.edu/2018/04/03/attention.html."""
    
    def __init__(self, h, d_model, dropout=0.1):
        "Take in model size and number of heads."
        super(MultiHeadedAttention, self).__init__()
        
        assert d_model % h == 0
        
        # We assume d_v always equals d_k
        self.d_k = d_model // h
        self.h = h
        self.linears = clones(nn.Linear(d_model, d_model), 4)
        self.attn = None
        self.dropout = nn.Dropout(p=dropout)
        
    def forward(self, query, key, value, mask=None):
        """Implements multihead attention"""
        if mask is not None:
            # Same mask applied to all h heads.
            mask = mask.unsqueeze(1)

        nbatches = query.size(0)
        
        # 1) Do all the linear projections in batch from d_model => h x d_k 
        query, key, value = \
            [l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
             for l, x in zip(self.linears, (query, key, value))]
        
        # 2) Apply attention on all the projected vectors in batch. 
        x, self.attn = attention(query, key, value, mask=mask, dropout=self.dropout)
        
        # 3) "Concat" using a view and apply a final linear. 
        x = x.transpose(1, 2).contiguous().view(nbatches, -1, self.h * self.d_k)

        return self.linears[-1](x)

This was a very high level overview of attention and transformers. If you want to dive deeper into how the Transformer works, I’d recommend The Illustrated Transformer, by Jay Alammar. Now let’s jump back into the Evoformer module:

The Evoformer architecture has two specialized transformers: one handles multiple sequence alignments (MSA), and the other manages pairwise interactions between amino acids.

The transformer for the MSA calculates attention over a vast matrix of individual amino acids in a protein sequence. To manage large computational cost, the attention mechanism has "row-wise" and "column-wise" components. This means the network first computes attention horizontally to identify related amino acid pairs, and then vertically to determine the most informative sequences.

Row-Wise Gated Self-Attention

A crucial aspect of AlphaFold 2's MSA transformer is the row-wise (horizontal) attention mechanism, which incorporates information from the "pair representation." When calculating attention, the network adds a bias term derived from the current pair representation, enhancing the attention mechanism's ability to identify interacting pairs of residues.

Additionally, note that when calculating similarities between queries and keys (amino acid residues), AlphaFold 2 utilizes not only information from the MSA embedding itself but also from the pair representation. The idea is that if two amino acid residues interact, this interaction is reflected in the pair representation. Row-wise self-attention leverages this information to update the MSA embedding accordingly.

Column-Wise Gated Self-Attention

Column-wise gated self-attention facilitates the exchange of information between sequences within an alignment column. This step helps AlphaFold 2 identify conserved or co-evolved positions and propagates data about the 3D structure from the first sequence in the alignment which is the sequence for which the structure is being predicted to the others.

Overall, the evoformer has two key points of communication for refining updates. The first is the bias, where the pair representation helps update the MSA. The second is the outer product mean block, where the MSA representation provides a way to update the pair representation.

The other transformer head that operates on the pair representation uses attention to process how residue pairs relate to one another in a graph representation. This graph is structured in terms of a triplet of amino acids (nodes) and their corresponding edges as seen here:

This setup enforces the use of the triangle inequality for pair distances to represent a 3D structure accurately. The pair representation is updated through a process called triangle multiplicative update, which updates an edge (distance between residues) based on the two other nodes and their edges. These three nodes are then updated using triangular self-attention. This mechanism allows the algorithm to learn further geometrical and chemical constraints, while triangular multiplicative updates ensure balanced attention across residues. Using these triangles and incorporating the "missing" connecting edge informs the positions of residues relative to global attractions, such as between partially charged residues that are distant in the sequence but might be close in the 3D form.

After several iterations (48 in the published model), the network constructs a model of the interactions within the protein. At this point, it is ready to build the 3D structure.

The structure module

So far, AlphaFold2 has generated two key representations: an MSA representation that captures sequence variation, and a "pairs" representation that identifies likely interactions between residues. The next challenge is to derive a structure from these representations, which is the task of the structure module.

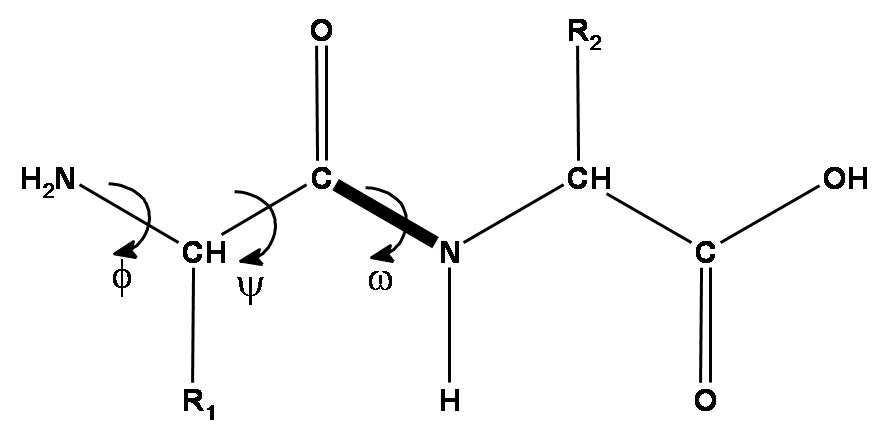
As a brief recap, a peptide chain is formed by amino acid residues. Each amino acid residue has three essential components: an amino group, a C-alpha atom, and a carboxyl group. These three groups form the protein backbone. Additionally, each amino acid has a side chain (R) that varies by amino acid type (we have 20 standard amino acids with a different side chain).

There are three torsion angles describing the backbone of each amino acid. The first two angles can vary widely, the third is almost always 180 degrees due to the nitrogen atom's electron pair. The length of the amino acid side chains varies, and they can also rotate around their atoms, contributing to their rotational angles.

DeepMind represents each residue as a triangle (the backbone frame), with the C-alpha atom at the vertex near the obtuse angle and the N and C atoms of the amino and carboxyl groups at the other vertices. The system predicts the shift of each residue relative to the global coordinate system and a 3x3 rotation matrix for the triangle's angle. The backbone is primarily predicted and side chain angles are handled by a ResNet.

The backbone frames start at the origin and are updated using information from the sequence embedding, derived from the MSA embedding, pair representation, and backbone frames, via the Invariant Point Attention (IPA) module. The IPA module combines these sources to predict residue coordinates, merging this with previous structural data and applying attention to the coordinates.

The IPA module does not update the 3D structure directly but updates the sequence embedding. The backbone update module then performs the 3D structure update, predicting the translation vector and rotation matrix for each residue based on the updated sequence embedding from the IPA.

Once the neural network predicts the 3D structure, the OpenMM package is used to relax the structure using different physical methods.

Losses: Frame Aligned Point Error and auxiliary

The main loss function used in training AF2 is called Frame Aligned Point Error (FAPE). FAPE is invariant to changes in the global coordinate frame, meaning changes in viewpoint do not affect the predicted protein structure. It combines the L2-norm with various regularizations and other techniques.

The final training loss is a weighted average of FAPE and additional auxiliary losses.

These are the losses from AF2:

Latest Model: AlphaFold3

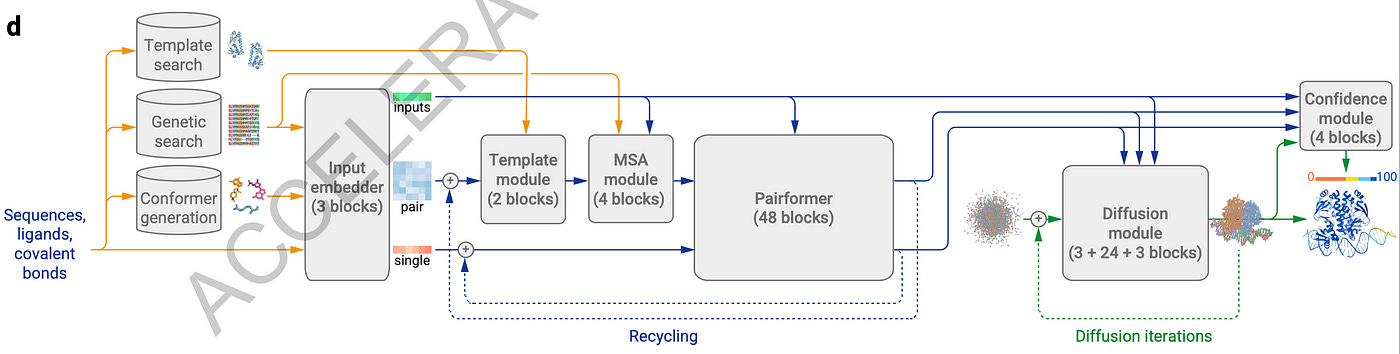
Very recently (May 8th, 2024), DeepMind and Isomorphic Labs published AlphaFold3. While AlphaFold3 is more accurate than AlphaFold2 in predicting single protein structures, its main advantage is its extension to predicting the structures of proteins, DNA, RNA, ligands, and other biomolecules.

Several significant enhancements have been introduced in the transition from AlphaFold2 to AlphaFold3. The most notable change is the replacement of the Structure module with a Diffusion module, which leads to improved predictions without imposing invariant or equivariant constraints. Another key advancement is including not only amino acids but also nucleotides for RNA and DNA, as well as heavy atoms representing diverse chemical molecules such as ligands. Unlike AlphaFold2, the MSA module in AlphaFold3 is also substantially smaller.

Here’s an overview of AlphaFold3:

This is the algorithm:

Similar to the structure in AlphaFold2, the architecture in AlphaFold3 relies on transformers. I’ll be walking through the high-level of how the main aspects of the algorithm work for the rest of the article.

Tokenization and Embeddings

The process of converting input molecules into a mathematical form involves several steps to ensure accurate representation for models like AlphaFold3. Different tokens are assigned to molecules such as proteins, RNA, DNA, and small molecules. Proteins are represented by amino acid tokens, while DNA and RNA are represented by nucleotides, and general molecules by single heavy atoms.

Each token has specific features that need embedding, including attributes like residue number, chain index, residue type, and conformer features like atom positions and charges. Multiple sequence alignment (MSA) features and template structures are also embedded. The AtomAttentionEncoder algorithm processes all-atom features, calculates relative distances, and uses multi-head cross-attention for contextual embeddings.

The embeddings are refined through linear transformations and pairwise token embeddings, including relative positional encodings to account for token order and position. User-defined bonds between tokens are integrated to enhance the representation of complex molecular interactions. This embedding process prepares the input features for the rest of the AF3 pipeline.

Template Embedder module

In AF3, the Template Embedder module utilizes pairwise embeddings from the previous step to focus on important regions within template structures obtained from template searches. Features extracted from the templates, including backbone frame masks, distograms, residue types, pseudo-beta masks, and unit vectors, are concatenated and processed through PairformerStack blocks. The resulting embeddings are added to the initial pairwise embeddings from the previous step and normalized before further modification. This iterative process ensures that the attention is directed towards significant structural changes in the protein templates.

MSA Module

Unlike AlphaFold2, which used 48 blocks, AlphaFold3 uses only four blocks in its MSA module.

The MSA module generates new subsets of the multiple sequence alignment (MSA) in each iteration by selecting MSAs randomly and processing their representations through a series of blocks. Unlike AF2, AlphaFold3's MSA module does not employ row-wise gated self-attention. Instead, attention is performed independently for each row, focusing more on pair representations. This change allows for better representation of residue pair interactions within rows of the MSA, contributing to improved model performance.

Pairformer module

In AlphaFold3, the Pairformer module replaces the Evoformer module from AlphaFold2, utilizing single representations from previous iterations and pair representations from the MSA module as input. Pairformer does not use explicitly use MSA data, as the MSA information is already embedded in the pair representations. The Pairformer stack consists of triangular update layers, triangular self-attention layers, and transition layers. Unlike Evoformer, which applied column-wise attention to MSA subsets, Pairformer applies row-wise attention to single sequences and effectively captures pair-wise interactions between tokens.

Diffusion module

The Diffusion module in AlphaFold3 replaces the Structure module from AlphaFold2, generating a distribution of structures by taking single and pair representations from the Pairformer module along with features and input embeddings. Initially, positions are generated from a Gaussian distribution around the origin, and various noises are applied to these positions, which are then processed through the Diffusion module. This module uses the AtomAttentionEncoder to update single and pairwise embeddings and noisy positions through linear layers and residual connections. The Atom Transformer applies local atom attention within the pairwise matrices, using a Diffusion Transformer with 24 blocks to denoise the structure at the atomic level.

This denoising process is further refined by applying self-attention at the token level, generating final token representations, which are converted into atom representations by the Atom Attention Decoder. The updated positions from the Atom Transformer are rescaled and combined with the noisy atom positions to produce new, denoised atom positions. The diffusion model excels in predicting local structures and accurately modeling side-chain geometries, even in regions with high noise levels.

Overall, the Diffusion model in AlphaFold3 predicts true atomic coordinates from noisy ones. However, confidence in the predicted structures is ensured through a subsequent Confidence module.

Confidence module and predictions

In AlphaFold3, the Confidence Head module assesses the reliability of structure predictions by using single and pair representations from the Pairformer module, predicted coordinates from the Diffusion module, and single inputs from the Input embedder. It evaluates confidence by embedding distances between token pairs and passing these through multiple blocks and predicting various metrics like predicted local distance difference test (pLDDT), pairwise atom-atom aligned error (PAE), predicted distance error (PDE), and resolution to the experimentally resolved ground truth. Additionally, the Distogram Head calculates the predicted binned distances between pairs of representative atoms. AlphaFold3 finally outputs the predicted coordinates, distogram probabilities, and confidence values.

Conclusion

Similar to the previous versions of AlphaFold, AlphaFold3 is the new SOTA method for protein structure prediction that has expanded predictions to DNA, RNA, ligands and other biomolecules. Tools like AlphaFold and other ML methods for protein structure understanding are critical for drug discovery, materials science, and personalized medicine by enabling insights into molecular interactions mechanisms.

As part of my next blogs, I’m hoping to dive deeper into AlphaFold3, RosettaFold and ESMFold. Any feedback/thoughts on this would be appreciated!

---

References

https://www.blopig.com/blog/2021/07/alphafold-2-is-here-whats-behind-the-structure-prediction-miracle/

https://borisburkov.net/2021-12-25-1/

https://www.nature.com/articles/s41586-021-03819-2

https://arxiv.org/abs/1706.03762

https://medium.com/@falk_hoffmann/alphafold3-and-its-improvements-in-comparison-to-alphafold2-96815ffbb044

https://www.nature.com/articles/s41586-024-07487-w